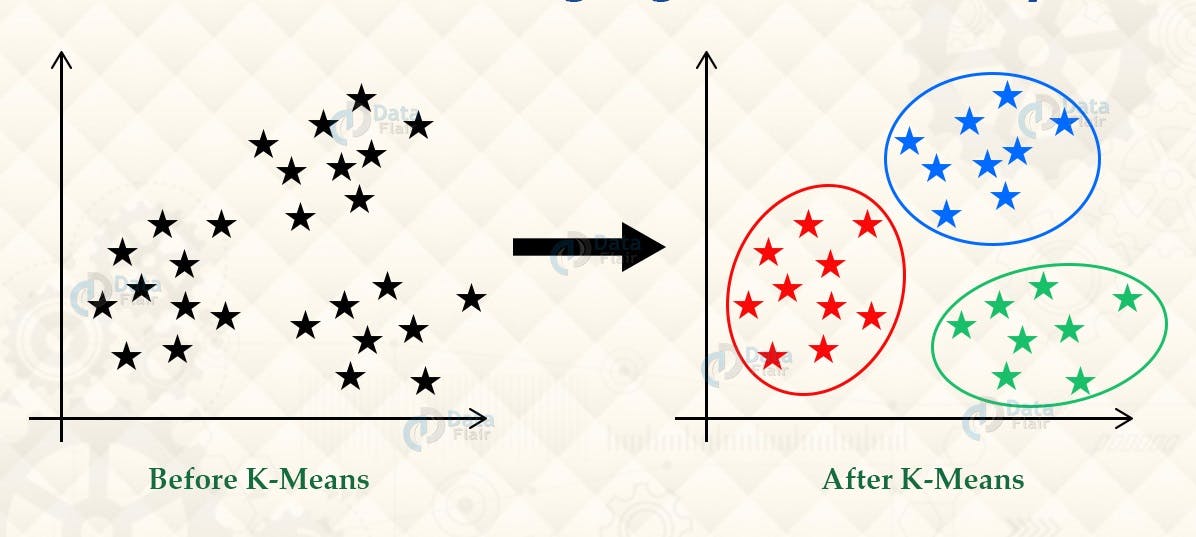
What is k-mean Clustering?

So, k-means clustering is a vector quantization method that seeks to split 'n' observations into 'k' clusters, with each observation belonging to the cluster with the nearest mean (cluster centers or cluster centroid), which serves as the cluster's prototype.

As a result, the data space is partitioned into Voronoi cells. Within-cluster variances (squared Euclidean distances) are minimized by k-means clustering, but regular Euclidean distances are not, which is the more difficult Weber problem: the mean optimizes squared errors, while only the geometric median reduces Euclidean distances. Using k-medians and k-medoids, for example, better Euclidean solutions can be obtained.

So what does this actually means? We can understand this as by considering a region, where a hospital care chain plans to open a series of emergency-care wards. We assume that the hospital is aware of all of the region's most accident-prone areas. They must decide on the number of Emergency Units to be opened as well as their location, so that all accident-prone locations in the vicinity of these Emergency Units are covered.

The problem is to select where these Emergency Units should be stationed so that the entire region is covered. This is where K-means Clustering can help! So we need to make a group of locations where these Units will be helpful. One Emergency Unit will be covering a group of locations or cluster of location, and total units established will be the number of cluster established. So if k clusters are to be established, it can be solved by the k-means clustering.

Method for k-mean Clustering

If k is given, the K-means algorithm can be executed in the following steps:

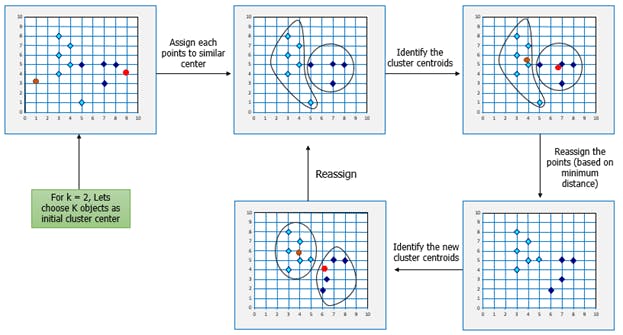
• Partition of objects into k non-empty subsets

• Identifying the cluster centroids (mean point) of the current partition.

• Assigning each point to a specific cluster

• Compute the distances from each point and allot points to the cluster where the distance from the centroid is minimum.

• After re-allotting the points, find the centroid of the new cluster formed.

Use-case in Security Domain

k-mean clustering is helpful in real world as well as technological world too. We can now study various examples of k-mean clustering in security domain alone.

1. Crime Localities Identification

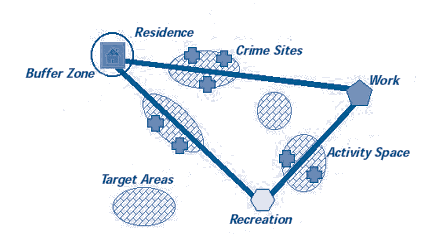The category of crime, the area of the crime, and the relationship between the two can provide qualitative insight into crime-prone areas within a city or a locality when data relating to crimes is accessible in specific locales within a city.

2. Classifying Crime Document

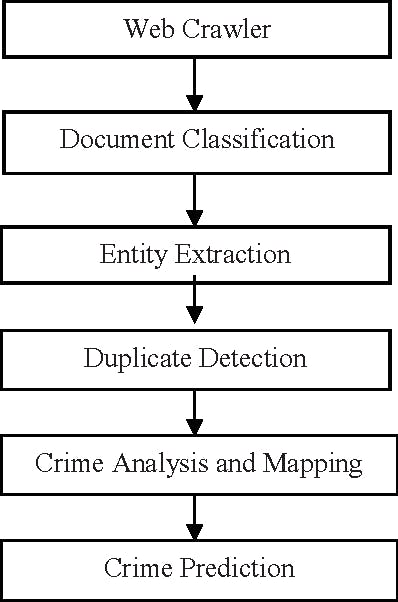Documents are grouped into several categories based on tags, subjects, and the document's content. This is a relatively common classification problem, and k-means is an excellent technique for it. The initial processing of the documents is required in order to represent each document as a vector and to find regularly used phrases that aid in document classification. The document vectors are then grouped to aid in the identification of document groupings that are comparable.

3. Clustering of IT Alerts

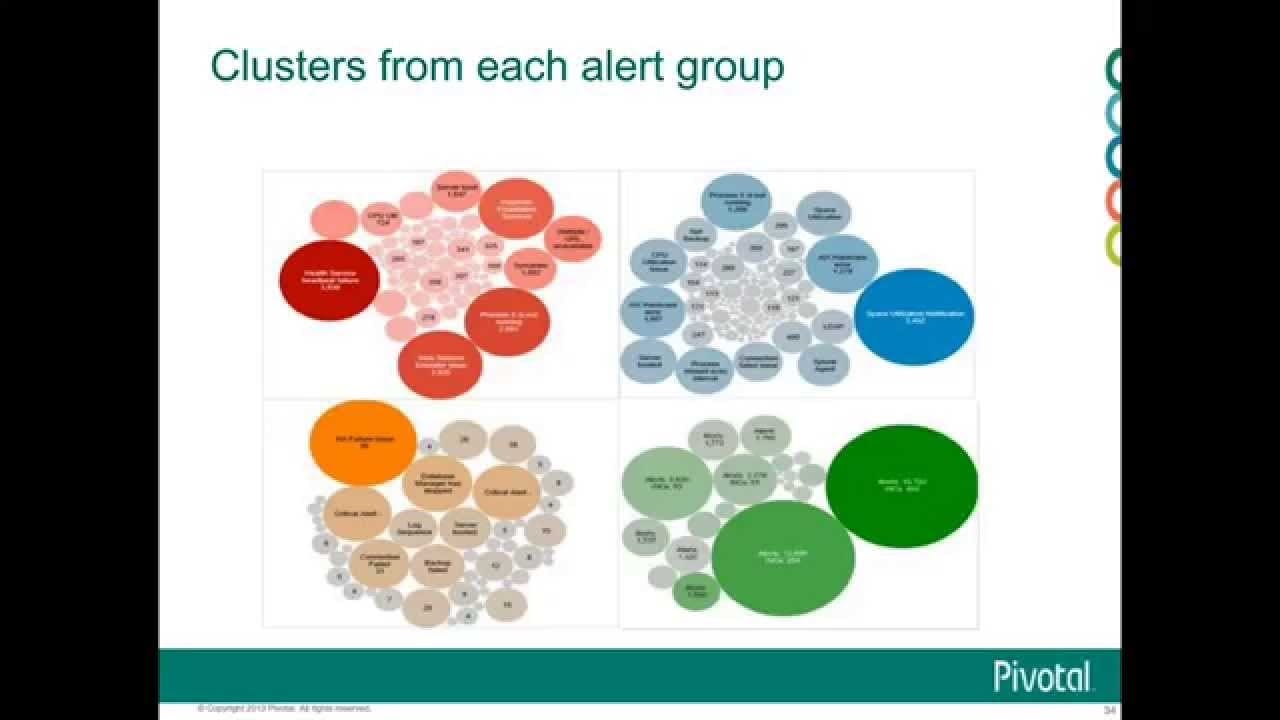Large company IT infrastructure technology components like network, storage, and databases create a lot of warning notifications. Because alert signals may indicate operational difficulties, they must be manually evaluated for downstream process prioritisation. Data clustering can provide insight into alarm categories and mean time to repair, as well as aid in failure prediction.